Fashion Nova Green Dresses: Stylish Looks for Every Occasion

Unraveling the Roots: A Comprehensive Exploration of Quadratic Equations with Four Terms

Unraveling the Roots: A Comprehensive Exploration of Quadratic Equations with Four Terms

Introduction

With great pleasure, we will explore the intriguing topic related to Unraveling the Roots: A Comprehensive Exploration of Quadratic Equations with Four Terms. Let’s weave interesting information and offer fresh perspectives to the readers.

Unraveling the Roots: A Comprehensive Exploration of Quadratic Equations with Four Terms

The realm of algebra, with its intricate equations and elegant solutions, often presents challenges, particularly when dealing with quadratic expressions. While the standard quadratic formula, designed for equations with three terms, provides a powerful tool for solving these equations, the presence of four terms introduces a new layer of complexity. This article delves into the intricacies of quadratic equations with four terms, exploring their unique characteristics, the methods for solving them, and their significance in various mathematical and real-world applications.

Understanding the Nature of Quadratic Equations with Four Terms

A quadratic equation is defined by its highest power of the variable, which is two. The standard form of a quadratic equation is ax² + bx + c = 0, where ‘a’, ‘b’, and ‘c’ are coefficients, and ‘x’ represents the unknown variable. However, when we encounter an equation with four terms, it takes the form ax² + bx + cx + d = 0. The presence of the additional term ‘d’ significantly alters the equation’s structure and necessitates a different approach to finding its solutions.

Methods for Solving Quadratic Equations with Four Terms

Solving quadratic equations with four terms involves a combination of techniques that aim to simplify the equation and reduce it to a standard quadratic form. The most common methods include:

1. Factoring by Grouping: This method involves grouping the terms in pairs and factoring out common factors. For example, in the equation 2x² + 3x – 8x – 12 = 0, we can group the first two terms and the last two terms:

(2x² + 3x) + (-8x – 12) = 0

Factoring out ‘x’ from the first group and ‘-4’ from the second group, we get:

x(2x + 3) – 4(2x + 3) = 0

Now, we have a common factor of (2x + 3), which can be factored out:

(2x + 3)(x – 4) = 0

This equation now resembles the standard quadratic form, and we can find the solutions by setting each factor equal to zero:

2x + 3 = 0 or x – 4 = 0

Solving for ‘x’, we get:

x = -3/2 or x = 4

2. Completing the Square: This method involves manipulating the equation to create a perfect square trinomial on one side. To illustrate, consider the equation x² + 6x + 5 = 0. We can rewrite this equation as:

(x² + 6x) + 5 = 0

To complete the square, we take half of the coefficient of ‘x’ (which is 6), square it (9), and add it to both sides of the equation:

(x² + 6x + 9) + 5 – 9 = 0

This simplifies to:

(x + 3)² – 4 = 0

Now, we can solve for ‘x’ by isolating the squared term and taking the square root of both sides:

(x + 3)² = 4

x + 3 = ±2

x = -3 ± 2

Therefore, the solutions are:

x = -1 or x = -5

3. Using the Quadratic Formula: While the quadratic formula is designed for equations with three terms, it can be adapted to solve equations with four terms by first reducing them to the standard form. This involves combining like terms and rearranging the equation. For example, in the equation 3x² – 2x + 5x – 4 = 0, we can combine the ‘x’ terms to get:

3x² + 3x – 4 = 0

Now, we can apply the quadratic formula:

x = (-b ± √(b² – 4ac)) / 2a

where ‘a’ = 3, ‘b’ = 3, and ‘c’ = -4. Substituting these values, we get:

x = (-3 ± √(3² – 4 3 -4)) / (2 * 3)

x = (-3 ± √(57)) / 6

Therefore, the solutions are:

x = (-3 + √57) / 6 or x = (-3 – √57) / 6

Importance and Applications of Quadratic Equations with Four Terms

Quadratic equations with four terms hold significant importance in various mathematical and practical domains. Here are some key applications:

1. Optimization Problems: These equations are frequently used in optimization problems where we seek to find the maximum or minimum value of a function. For instance, in economics, quadratic equations can be used to model profit functions, where finding the maximum profit requires solving a quadratic equation with four terms.

2. Physics and Engineering: Quadratic equations play a crucial role in describing motion, projectile trajectories, and other physical phenomena. In engineering, they are employed in the design of structures, bridges, and other infrastructure.

3. Finance and Economics: Quadratic equations are used in financial modeling, particularly in calculating interest rates, loan repayments, and investment growth. In economics, they are utilized to analyze market demand, supply, and equilibrium points.

4. Computer Science and Artificial Intelligence: Quadratic equations are fundamental in computer science, particularly in algorithm design, data analysis, and machine learning. They are used to model and solve various optimization problems, such as finding the best fit line for a set of data points.

FAQs about Quadratic Equations with Four Terms

1. Can all quadratic equations with four terms be solved using the quadratic formula?

Not directly. The quadratic formula is designed for equations with three terms. However, by simplifying the equation with four terms to the standard form, we can then apply the quadratic formula.

2. What happens if the quadratic equation with four terms has no real solutions?

In such cases, the discriminant (b² – 4ac) in the quadratic formula will be negative. This indicates that the equation has complex solutions, which involve imaginary numbers.

3. Are there any special cases where quadratic equations with four terms can be solved easily?

Yes, if the equation can be factored by grouping, the solutions can be found quite easily.

4. What are some common mistakes to avoid when solving quadratic equations with four terms?

• Incorrectly grouping terms: Ensure that you group the terms in a way that allows for common factors to be extracted.
• Neglecting to simplify the equation: Before applying the quadratic formula, simplify the equation to the standard form.
• Misinterpreting the solutions: Make sure to correctly interpret the solutions, considering both positive and negative values.

Tips for Solving Quadratic Equations with Four Terms

• Identify the common factors: Look for common factors in the terms that can be factored out.
• Simplify the equation: Combine like terms and rearrange the equation to the standard form.
• Use the appropriate method: Choose the method that best suits the specific equation, considering factoring, completing the square, or the quadratic formula.
• Check your solutions: Substitute the solutions back into the original equation to verify their validity.

Conclusion

Quadratic equations with four terms, while seemingly more complex than their three-term counterparts, can be effectively solved using a combination of techniques, including factoring by grouping, completing the square, and adapting the quadratic formula. These equations play a crucial role in various mathematical and real-world applications, demonstrating their importance in optimizing processes, modeling physical phenomena, and driving advancements in diverse fields. Understanding the methods for solving these equations empowers us to tackle complex problems and unlock new insights in mathematics and beyond.

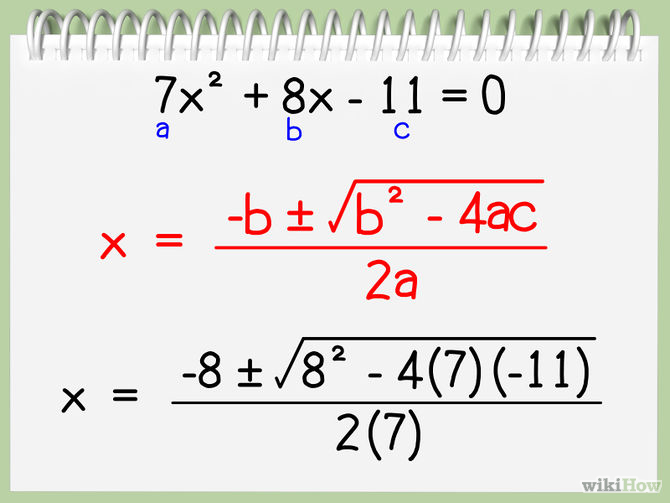
Closure

Thus, we hope this article has provided valuable insights into Unraveling the Roots: A Comprehensive Exploration of Quadratic Equations with Four Terms. We appreciate your attention to our article. See you in our next article!